Abstract
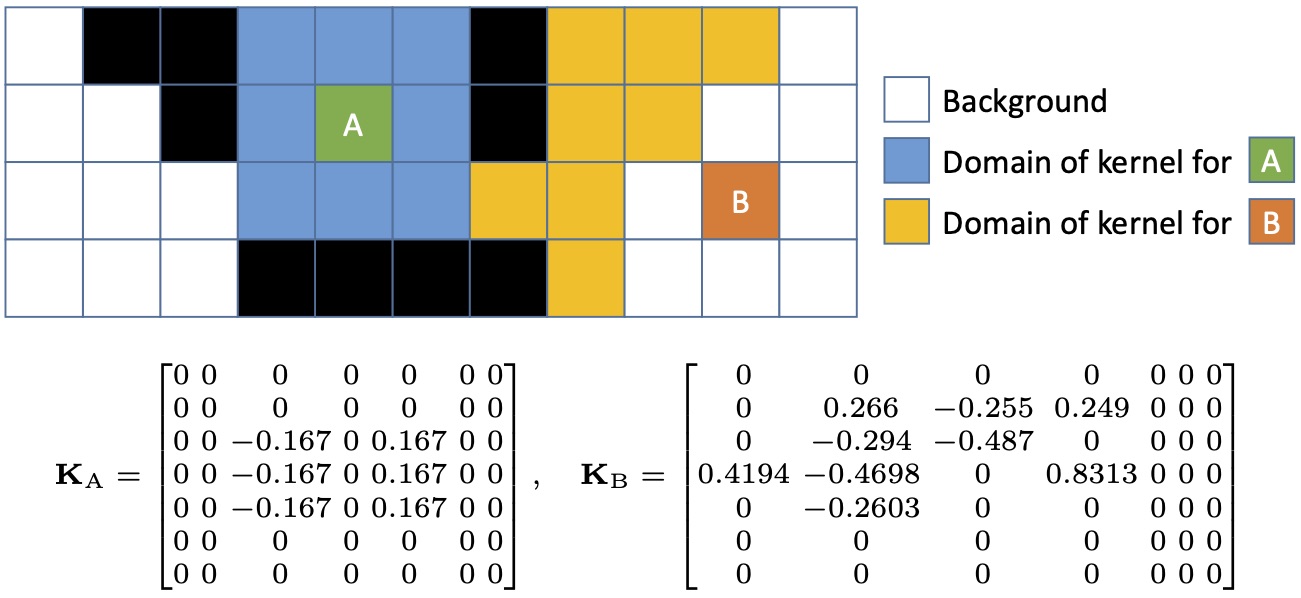
Almost universally in computer vision, when surface derivatives are required, they are computed using only first order accurate finite difference approximations. We propose a new method for computing numerical derivatives based on 2D Savitzky-Golay filters and K-nearest neighbour kernels. The resulting derivative matrices can be used for least squares surface reconstruction over arbitrary (even disconnected) domains in the presence of large noise and allowing for higher order polynomial local surface approximations. They are useful for a range of tasks including normal-from-depth (i.e. surface differentiation), height-from- normals (i.e. surface integration) and shape-from-x. We show how to write both orthographic or perspective height-from-normals as a linear least squares problem using the same formulation and avoiding a nonlinear change of variables in the perspective case. We demonstrate improved performance relative to state-of-the-art across these tasks on both synthetic and real data and make available an open source implementation of our method.