- Named after Benoit B. Mandelbrot.
- A fractal generated by iterating: \( z_{n+1} = z_n^2 + c; z_0=0 \), and plotting how fast it diverges to infinity for different values of the complex number \(c\) (speed of divergence represented by colours). The black set represents the “prisoner” points that do not diverge: it is the Mandelbrot set.
 |
Mandelbroids
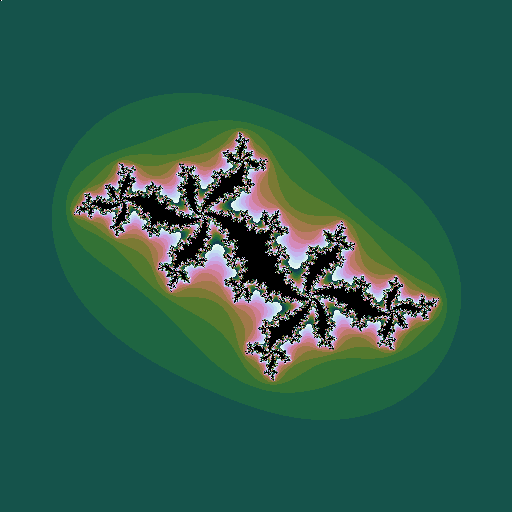
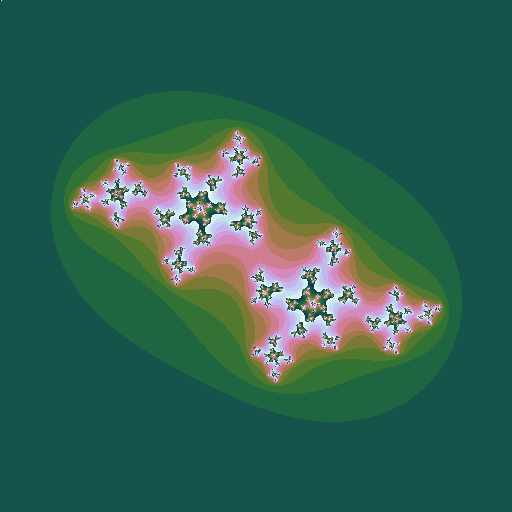
- Other related Mandelbrots can be generated by iterating \(z^k+c\), for different values of \(k\).
- For higher integer \(k\), each Mandelbrot ‘bud’ becomes \(k-1\) buds.
- For non-integer \(k\), the picture has discontinuities. We are taking roots, which process gives several solutions, but we are looking at only one of them.
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
| \(k = 1 .. 6\), step \(0.05\) | \(k = 1 .. 3\), step \(0.02\) | \(k = 1.8 .. 2.2\), step \(0.05\) |
Buddhabrot
- The iterative algorithm for calculating the Mandelbrot set gives a trajectory for each point. Some trajectories diverge to infinity, some do not. But what is the trajectory during the iteration?
- Consider all the starting points outside the Mandelbrot set, and plot the points visited along the way to escape on each trajectory. This gives the so-called Buddhabrot plot. (It is conventional to plot these rotated by 90 degrees.)
- The plots below show the distribution of trajectories that have escaped by 1000 iterations, for \(42\) million randomly chosen values of \(c\). Dark regions have few points; light regions have more points.
- Conversely, consider all the starting points inside the Mandelbrot set, and plot the points visited along the way to to determining they do not escape (up to some maximum number of iterations). This gives the so-called Anti-Buddhabrot plot.
- The plots below show the distribution of trajectories that have not escaped by 1000 iterations, for \(42\) million randomly chosen values of \(c\).
| \(c = 0.1 + 0.5i\) Starting at a point deep inside the set, the trajectory rapidly converges |
 |
|
| \(c = 0.1 + 0.6i\) Starting at a point inside, near the boundary, the trajectory cycles |
 |
|
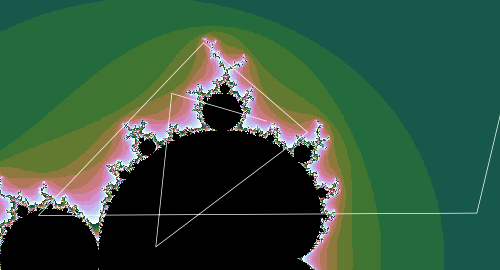
| \(c = 0.1 + 0.6i\) Starting at a point outside the set, the trajectory diverges, but does visit points inside the set |
 |
 |
 |
 |
 |
 |
 |