Base ten representation: n = d r d r -1 ... d 0
Then n is divisible by the listed number, if
- d 0 divisible by 2
- sum of the digits divisible by 3
- d 1 d 0 divisible by 4
- d 0 divisible by 5
- divisible by 2 and by 3
-
d
r
...
d
1
-
2×
d
0
divisible by 7
Example 4319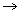 431 - 2×9 = 413
431 - 2×9 = 413
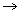 41 - 2×3 = 35 = 5×7
41 - 2×3 = 35 = 5×7
If d r ... d 1 - 2× d 0 = m ×7, then d r ... d 1 d 0 = (10× m +3× d 0 )×7
Example 413 = (10×5+3×3)×7 = 59×7 and then 4319 = (10×59+3×9)×7 = 617×7 - d 2 d 1 d 0 divisible by 8
- sum of the digits divisible by 9
- d 0 = 0
- sum of the even digits, minus sum of the odd digits, divisible by 11
- divisible by 3 and by 4
-
d
r
...
d
1
-
9×
d
0
divisible by 13
Example 4316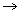 431 - 9×6 = 377
431 - 9×6 = 377
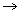 37 - 9×7 = -26 = -2×13
37 - 9×7 = -26 = -2×13
If d r ... d 1 - 9× d 0 = m ×13, then d r ... d 1 d 0 = (10× m +7× d 0 )×13
Example 377 = (10×-2+7×7)×13 = 29×13 and then 4316 = (10×29+7×6)×13 = 332×13 - d 1 d 0 divisible by 25
Fast algorithm for prime factors:
-
d
0
+ 3×
d
1
+ 2×
d
2
-
d
3
- 3×
d
4
- 2×
d
5
... divisible by 7, where the coefficient
c
n
of digit
d
n
is 10
n
mod 7
(taking the closest result to zero, rather than a positive result, to
help the sum cancel)
Example 4319 9 + 3×1 +2×3 - 4 = 14 = 2×7
9 + 3×1 +2×3 - 4 = 14 = 2×7
-
d
0
- 3×
d
1
- 4×
d
2
-
d
3
+ 3×
d
4
+ 4×
d
5
... divisible by 13, where the coefficient
c
n
of digit
d
n
is 10
n
mod
13
Example 4316 6 - 3×1 - 4×3 - 4 = -13
6 - 3×1 - 4×3 - 4 = -13
- The technique can be used for divisibility by any prime p , where the coefficient c n of digit d n is 10 n mod p .
- The earlier rules for 2, 3, 5 and 11 are special cases of this rule, where the coefficients have a simple pattern.