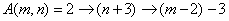- John Baez's Azimuth blog Enormous Integers page
- Robert P. Munafo's Large Numbers pages
- Sbiis Saibian's Large Number Site
- my review of Bloch's The Unimaginable Mathematics of Borges' Library of Babel
Knuth's up-arrow notation
In 1976 Donald Knuth published his up-arrow notation for large numbers. The arrows 'associate to the right' (following exponentiation). So a ^ b ^ c ^ d means a ^( b ^( c ^ d )), etc. This association gives the largest value.
- m n = m + m + ... + m ( n terms) = m × n
-
m
^
n
=
m
m
...
m
(
n
terms) =
m
n
- m ^1 = m
-
m
^
n
=
m
(
m
...
m
(
n
-1
terms)) =
m
m
^(
n
-1)
- 2^2 = 2×2 = 4; 2^3 = 2×2^2 = 8; 2^4 = 2×2^3 = 16; etc...
- 3^2 = 3×3 = 9; 3^3 = 3×3^2 = 27; 3^4 = 3×3^3 = 81; etc...
- 4^2 = 4×4 = 16; 4^3 = 4×4^2 = 64; 4^4 = 4×4^3 = 256; etc...
-
m
^^
n
=
m
^
m
^...^
m
(
n
terms) =
m
m
...
m
- m ^^1 = m
-
m
^^
n
=
m
^(
m
^...^
m
(
n
-1
terms)) =
m
^
m
^^(
n
-1)
- 2^^2 = 2^2 = 4
- 2^^3 = 2^2^^2 = 2^4 = 16
- 2^^4 = 2^2^^3 = 2^16 = 65536
- 3^^2 = 3^3 = 27
- 3^^3 = 3^3^^2 = 3^27 = 7625597484987
- 3^^4 = 3^3^^3 = 3^7625597484987
- 4^^2 = 4^4 = 256
- 4^^3 = 4^4^^2 = 4^256
- 4^^4 = 4^4^^3 = 4^4^256
-
m
^^^
n
=
m
^^
m
^^...^^
m
(
n
terms)
- m ^^^1 = m
-
m
^^^
n
=
m
^^(
m
^^ ... ^^
m
(
n
-1 terms)) =
m
^^
m
^^^(
n
-1)
- 2^^^2 = 2^^2 = 4
- 2^^^3 = 2^^2^^^2 = 2^^4 = 65536
- 2^^^4 = 2^^2^^^3 = 2^^65536 = 2^2^...^2 (65536 terms)
- 3^^^2 = 3^^3 = 7625597484987
- 3^^^3 = 3^^3^^^2 = 3^^7625597484987 = 3^3^...^3 (7625597484987 terms)
-
3^^^4 = 3^^3^^^3 = 3^^3^...^3 (7625597484987 terms)
= 3^...^3 (3^...^3 (7625597484987 terms) terms) - 4^^^2 = 4^^4 = 4^4^256
- 4^^^3 = 4^^4^^^2 = 4^^4^4^256 = 4^...^4 (4^4^256 terms)
- 4^^^4 = 4^^4^^^3 = 4^^4^...^4 (4^4^256 terms)
-
m
^^^^
n
=
m
^^^
m
^^^...^^^
m
(
n
terms)
- m ^^^^1 = m
-
m
^^^^
n
=
m
^^^(
m
^^^ ... ^^^
m
(
n
-1 terms)) =
m
^^^
m
^^^^(
n
-1)
- 2^^^^2 = 2^^^2 = 4
- 2^^^^3 = 2^^^2^^^^2 = 2^^^4 = 2^2^...^2 (65536 terms)
- 2^^^^4 = 2^^^2^^^^3 = 2^^^2^2^...^2 (65536 terms)
- 3^^^^2 = 3^^^3 = 3^3^...^3 (7625597484987 terms)
-
3^^^^3 = 3^^^3^^^^2 = 3^^^3^3^...^3 (7625597484987 terms)
= 3^^3^3^...^3 (3^3^...^3 (7625597484987 terms) terms) - 4^^^^2 = 4^^^4 = 4^^4^...^4 (4^4^256 terms)
- etc...
-
googol
- googol = 10 100 = 10 ^ 10 ^ 2
- googolplex = 10 googol = 10 ^ 10 ^ 10 ^ 2
- Skewes' number , = e e e 79 , approx 10 10 10 34 , < 4^^5, occurs in theories on the distribution of primes
-
The up-arrow notation has a close relationship to the
Ackermann
function
:
- A (1, n ) = 2 + ( n + 3) - 3
- A (2, n ) = 2 ( n + 3) - 3
- A (3, n ) = 2 ^ ( n + 3) - 3
- A (4, n ) = 2 ^^ ( n + 3) - 3
- A (5, n ) = 2 ^^^ ( n + 3) - 3
- etc...
-
Graham's number
is constructed thus:
- Construct G 1 = 3^^^^3
- Construct G 2 = 3^^...^^3, where there are G 1 up-arrows
- Construct G 3 = 3^^...^^3, where there are G 2 up-arrows.
- ...
- Graham's number G = 3^^...^^3, where there are G 63 up-arrows.
Eventually, as for cases like Graham's number, you get too many up-arrows to manipulate easily. Something more extensible is needed.
Conway's chained arrow notation
John H. Conway has gone 'one' step further:
-
a
 b
b
 c
=
a
^^...^^
b
, with
c
up arrows
c
=
a
^^...^^
b
, with
c
up arrows
-
The chain can be reduced in length when the last item is a 1
a b
b
 ...
x
...
x
 1 =
a
1 =
a
 b
b
 ...
x
...
x
-
The last item in the chain can be reduced in size by 1
a ... x y
y
 (
z
+ 1) depends on
y
:
(
z
+ 1) depends on
y
:
-
a
...
x
 1
1
 (
z
+ 1) =
a
...
x
(
z
+ 1) =
a
...
x
-
a
...
x
 2
2
 (
z
+ 1) =
a
...
x
(
z
+ 1) =
a
...
x
 (
a
...
x
)
(
a
...
x
)
 z
z
-
a
...
x
 3
3
 (
z
+ 1) =
a
...
x
(
z
+ 1) =
a
...
x
 (
a
...
x
(
a
...
x
 (
a
...
x
)
(
a
...
x
)
 z
)
z
)
 z
z
- etc... (where the brackets can be removed once the number inside has been evaluated)
-
a
...
x
-
Ackermann's function
becomes even easier to express in right-arrow notation:
-
-
3
 3
3
 64
64
 2 <
Graham's number
<
3
2 <
Graham's number
<
3
 3
3
 65
65
 2 < 3
2 < 3
 3
3
 3
3
 3
3
Eventually, you get too many right arrows to manipulate easily. Something more extensible is needed...
Steinhaus's polygon notation
It is easy to write down very large numbers. Such giants can be defined very simply if we agree to write
instead of a a ,
instead of ' a in a triangles', and
instead of ' a in a squares'. Then the number 'Mega' =
is already too great to have any physical meaning,
![[Mega] [Mega]](mega.jpg)
the last symbol being 256 in 256 triangles, and the reason why we have abandoned the ordinary system of writing numbers is clear. (The reader may try to explain the 'Megiston' given by
).
-- H. Steinhaus. Mathematical Snapshots , Ch.1, 3rd edn. 1983 [note that there is an error in the diagram as printed: it should read ... =
= ...]
Moser's polygon notation
Leo Moser extended Steinhaus' notation. Rather than going to a circle for the third level, Moser continues the sequence of polygons with a pentagon, an hexagon, and so on. So we have
-
![[a in triangle] [a in triangle]](atri.jpg) =
a
a
=
a
a
-
![[a in square] [a in square]](asq.jpg) = '
a
in
a
triangles'
= '
a
in
a
triangles'
-
![[a in pentagon] [a in pentagon]](apent.jpg) = '
a
in
a
squares'
= '
a
in
a
squares'
- and so on
In order to express general relationships, it is useful to have a
rather different notation, than captures the number of sides of the
polygons, and the number of repetitions of the polygons, symbolically.
So, instead of drawing the polygon, I write the number of sides in
square brackets:
![]() =
a
[3];
=
a
[3];
![]() =
a
[3][4], etc. And instead of drawing repeated similar
polygons, I subscript the 'polygon number' with the repetition number:
=
a
[3][4], etc. And instead of drawing repeated similar
polygons, I subscript the 'polygon number' with the repetition number:
![]() =
a
[3][3] =
a
[3]
2
;
=
a
[3][3] =
a
[3]
2
;
![]() =
a
[3][3][4][4][4] =
a
[3]
2
[4]
3
,
etc. This means we can define the notation in general:
=
a
[3][3][4][4][4] =
a
[3]
2
[4]
3
,
etc. This means we can define the notation in general:
-
![[a in triangle] [a in triangle]](atri.jpg) =
a
[3] =
a
a
=
a
[3] =
a
a
-
![[a in square] [a in square]](asq.jpg) =
a
[4] = '
a
in
a
triangles' =
a
[3]
a
=
a
[4] = '
a
in
a
triangles' =
a
[3]
a
-
![[a in pentagon] [a in pentagon]](apent.jpg) =
a
[5] = '
a
in
a
squares' =
a
[4]
a
=
a
[5] = '
a
in
a
squares' =
a
[4]
a
- a [ k +1] = ' a in a k -gons' = a [ k ] a
The polygons associate to the left, and bind more strongly that conventional mathematical operators. So n [2]^ n [3] means ( n [2])^( n [3]). Expanding deeply nested terms from the inside out (expand the definition of the innermost polygon first), or from the outside in (expand the definition of the outermost polygon first) gives the same result.
-
![[a in triangle] [a in triangle]](atri.jpg) =
a
[3] =
a^a
=
a
[3] =
a^a
- n [3] = n^n
- n [3] 2 = n [3][3] = n [3]^ n [3] = ( n^n )^( n^n )
- n [3] 3 = n [3] 2 [3] = n [3] 2 ^ n [3] 2 = (( n^n )^( n^n ))^(( n^n )^( n^n ))
- n [3] 4 = n [3] 3 [3] = n [3] 3 ^ n [3] 3 = ((( n^n )^( n^n ))^(( n^n )^( n^n )))^((( n^n )^( n^n ))^(( n^n )^( n^n )))
- n [3] k = (...( n^n )^( n^n )...)^...^(...( n^n )^( n^n )...)[2 k terms]
- 2[3] = 2^2 = 4
- 2[3] 2 = 2[3]^2[3] = 4^4 = 256
- 2[3] 3 = 2[3] 2 ^2 2 [3] = 256^256 = 10 616.509...
- 2[3] 4 = 2[3] 3 ^2 3 [3] = 10 616.509... ^10 616.509... = 10 616.509... x 10 616.509... = 10 10 619.3...
- 2[3] 5 = 2[3] 4 ^2[3] 4 = 10 10 619.3... ^10 10 619.3...
- etc..
- 3[3] = 3^3 = 27
- 3[3] 2 = 3[3]^3[3] = 27^27 = 443426488243037769948249630619149892803 = 10 38.646...
- 3[3] 3 = 3[3] 2 ^3[3] 2 = 10 38.646... ^10 38.646... = 10 10 40.23...
- etc...
- 4[3] = 4^4 = 2[3]^2[3] = 2[3][3] = 2[3] 2
- 4[3] 2 = 4[3][3] = 2[3] 2 [3] = 2[3] 3
- 4[3] 3 = 4[3] 2 [3] = 2[3] 3 [3] = 2[3] 4
- 4[3] k = 2[3] k +1
-
![[a in square] [a in square]](asq.jpg) =
a
[4] =
a
[3]
a
=
a
[4] =
a
[3]
a
- n [4] = n [3] n = (...( n^n )^( n^n )...)^...^(...( n^n )^( n^n )...)[2 n terms]
- 2[4] = 2[3] 2 = 256
- 2[4] 2 = 2[4][4] = 256[4] = 256[3] 256
- 2[4] 3 = 2[4] 2 [4] = 256[3] 256 [4] = 256[3] 256 [3] 256[3] 256
- etc...
- 3[4] = 3[3] 3 = 3[3] 2 ^3[3] 2 = (27^27)^(27^27)
-
3[4]
2
= 3[3]
3
[4] = (3[3]
2
^3[3]
2
)[4]
= ((27^27)^(27^27))[4]
= ((27^27)^(27^27))[3] (27^27)^(27^27) - etc...
- 4[4] = 4[3] 4 = 2[3] 5
- etc...
-
![[a in pentagon] [a in pentagon]](apent.jpg) =
a
[5] =
a
[4]
a
=
a
[5] =
a
[4]
a
- 2[5] = Steinhaus' Mega = 2[4] 2 = 2[3] 2 [4] = (2^2)[3][4] = (4^4)[4] = 256[3] 256
- A polygon with 2[5] sides is a Megagon . It looks pretty circular if drawn!
- 2[5] 2 = 2[5][5] = 2[4] 2 = 256[3] 256 [5]
- 3[5] = 3[4] 3 = ((27^27)^(27^27))[3] (27^27)^(27^27) [4]
- 10[5] = Steinhaus' Megiston = 10[4] 10
- etc..
-
a
[6] =
a
[5]
a
- 2[6] = 2[5] 2 = 256[3] 256 [5]
- 3[6] = 3[5] 3 = 3[5][5] 2 = ((27^27)^(27^27))[3] (27^27)^(27^27) [4][5] 2
- in general, a [ k +1] = a [ k ] a
Moser's number = '2 in a Megagon' = 2[2[5]] = 2[256[3] 256 ]
Which of Moser's number and Graham's number is the larger? The Moser
construction yields big numbers
much
faster than does the
up-arrow notation, but there are a
lot
of up-arrows in the
Graham number.
- [7 July 1998] : Tim Chow has provided me with a clear outline proof that G >> M .
- Coincidentally, a few days later Todd Cesere, who was the first to suggest to me that "Graham's number is far larger than the Moser", also sent me a proof; it takes a similar approach to Chow's proof.