Abstract
Nanotechnology promises to deliver unparalleled benefits, but all these
benefits require sophisticated and subtle programming of the nano-machines
themselves. A swarm of benevolent nanites could increase our quality of
life immensely; a swarm of rogue nanites could spell disaster. What
computing paradigms are needed in order to help us gain the benefits while
eliminating the risks?
Studies in Artificial Life, investigating properties of complex systems
and emergent behaviour, help us understand how many small systems can
combine to form a large system with qualitatively different behaviour.
This understanding may pave the way to safe and robust programming of
nanites.
This talk explores and discusses these various issues.
Nanomachines
 Natural
size scales
Natural
size scales
We tend to think that "more complex" goes with "bigger"
-
nano - atoms
-
micro - big molecules, DNA (>> billion atoms)
-
milli - bacteria, cells
-
metre - animals and plants
Technology size scales
Our technology is decreasing in size, yet getting more complex
-
metre - big engineering, machines
-
milli - small components, nuts, bolts, chips
-
micro - chip components, gates, etc
-
nano - atomic scale - new stuff: components made of a few thousand
atoms
Nano manufacturing
Nano machines manipulate matter at the molecular and atomic level.
A cow is a machine for turning grass, water and air into beef. A nanite
could be designed to do the same thing directly. Pour grass into a hopper,
fill the tank with water, switch on the power, and let the nanites get to
work. A while later, open the door, and there's a steak!
In fact, nanites could in principle be designed to build just about
anything that can be build by manipulating matter.
But how can a sub-microscopic machine build anything as large as a
decent steak? It is is feasible because one of the things nanites could be
designed to build is themselves -- they could be made
self-replicating
.
So it is very easy to get enough nanites to build macroscopic objects.
Self-replication
 Can we ever
get enough nanites to build something macroscopic? What are
self-replication timescales? We can make some very rough estimates, using
2
10
~ 10
3
, so every 10 doublings, we would have a
1000 times as many nanites
Can we ever
get enough nanites to build something macroscopic? What are
self-replication timescales? We can make some very rough estimates, using
2
10
~ 10
3
, so every 10 doublings, we would have a
1000 times as many nanites
Ordinary cells can divide every 10 hours, embryonic cells every 10
minutes. So let's take a doubling time of 100 seconds (well over a
minute). If at
t
=0 we had one nanite consisting of 1000 atoms,
massing 10
-23
kg then,
if
enough raw material were
available:
-
6 x10
3
s (100 mins) 10
18
nanites, massing 10
-5
kg
-
7 x10
3
s (2 hrs) 10
21
nanites, massing 10
-2
kg = 10 grams
-
8 x10
3
s (2.2 hrs) 10
24
nanites, massing 10
1
kg
-
9 x10
3
s (2.5 hrs) 10
27
nanites, massing 10
4
kg
-
10 x10
3
s (2.7 hrs) 10
30
nanites, massing 10
7
kg = 10 tonnes
-
11 x10
3
s (3 hrs) 10
33
nanites, massing 10
10
kg = 10 000 tonnes
-
16 x10
3
s (4.4 hrs) 10
48
nanites, massing 10
25
kg = mass Earth
Nano applications
Pollution control
And it's not just building new things. Nanites can rearrange what is
already around. One quite exciting possibility is pollution control
-
For example, nanites could be designed to harvest heavy metals and
toxic chemicals from polluted sites
-
They could be seeded into the upper atmosphere to repair the holes in
the ozone layer
-
And since they can make just about anything, large unsightly
factories and manufacturing plants may well be made obsolete
Medical applications
As well as repairing the environment, eventually there might be nanites
that could repair you.
-
For example, some cancers may due to some damage in the cells.
Nanites could fix the damage
-
Some heart disease is caused by build up of cholesterol in the
arteries. Nanites could be put in your blood to go and scrub the artery
walls clean
-
Many diseases are caused by errors in the DNA. Nanites could fix
erroneous DNA, and could monitor cell division and fix any copying
problems
-
Some people are even talking about complete designer bodies,
eventually
Nano problems
Of course, all great advances come with associated problems. Before we
get all these advantages from nanotechnology, we have to think about how
we might solve these.
Nano viruses
One thing I mentioned is putting nanites in people, to help cure them of
diseases. But what if the nanites go wrong? They might
cause
diseases.
 Grey
goo
Grey
goo
The worst case scenario is known as the "grey goo" problem.
Rogue nanites might get loose and disassemble the world, reducing it to
grey goo.
Remember, we calculated that it took less than 5 hours for our
self-replicating nanites to become a mass the size of the earth (given
sufficient raw materials, of course...).
Safety critical programming
We will have to think about how we can program these nanites safely, so
that they won't go wrong.
You have probably all heard about some software disaster or other, where
something has gone horribly wrong. We are only just beginning to
understand the problems of writing large software.
Programming nanites could make other exercises in safety critical
programming look quite straightforward by comparison.
Programming nanites
And there are new kinds of problems if we want to program nanites.
-
How can we fit a large program into a little nanite, to get it to do
something as complicated as self-replication? How do we get a small
program to have a complex effect?
-
How can we get trillions of nanites to work together cooperatively,
without the crippling overheads of a centralised controller, to build
macroscopic structures?
The answers to these puzzles may lie in the new science of chaos,
complexity, and self-organising systems.
A classical view of science
First, a classical view of science:
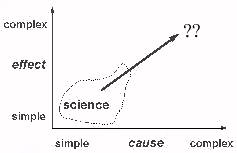
There are causes, that range from simple to complex, and there are
effects, that also range from simple to complex.
The classical view is that
simple causes result in simple effects
,
and
complex causes give complex effects
. In this view the world
falls along this diagonal line.
Science tries to find simple causes and underlying laws, so this seems
to necessarily mean it explains simple effects.
Depending how far up this line you go, the particular branch of science
has different names : physics at the bottom, then chemistry, then biology.
And right at the top, we have things just too difficult for us at the
moment.
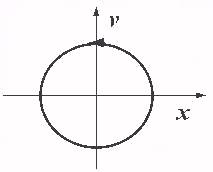 Classical
dynamics: attractors
Classical
dynamics: attractors
So the classical view says we have simple equations giving simple
behaviour.
For example,
a
+ w
x
= 0 -- Simple Harmonic Motion: the
equation describes the motion of a simple pendulum. The equation says that
the restoring force is proportional to the displacement.
The graph is a plot of position against velocity. When the displacement
is a maximum, the speed is zero. When the speed is a maximum, the
displacement is zero.
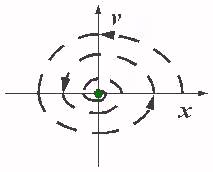
In the real world there is always friction
a
+ k
v
+ w
x
= 0 -- Damped Simple Harmonic
Motion
This is the equation for a damped pendulum, where the damping is
proportional to the speed. The maximum speed and maximum displacement get
smaller on each swing.
So if we plot this damped motion, it spirals down to the centre: no
speed, no displacement: it has stopped.
This is the classical view:
simple
equations describe
simple
behaviour.
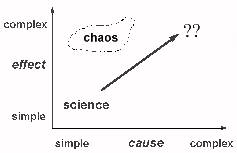 Chaos
Chaos
But the results of the new chaos science show us that this classical
intuition is just
false
. Simple causes can have profoundly complex
behaviours.
Coupled pendulums
[Here I demonstrated an 'executive toy', consisting
of a pair of coupled pendulums containing small magnets, which exhibits
fascinating chaotic behaviour.]
One reason why this science is so new is that it relies heavily on
computers to explore the complex behaviour of simple equations. One might
cynically think that the reason why it was thought simple equations have
simple behaviours is that scientists only investigated equations they
could solve by hand, which necessarily had simple solutions!
 Logistic
mapping
Logistic
mapping
x
n
+1
= lambda
x
n
(1-
x
n
)
Let's plot the
x
n
as a function of lambda.
[Here I ran a
numerical
simulation
, which allowed the solution to build up slowly with
increasing lambda, and talked through the features as they appeared.]
For small lambda, we do get equilibrium. Larger lambda, we get a
bifurcation, or a period doubling. One year there is a big population,
then a small one, then a big one. 'Boom and bust' cycles. As lambda
continues to grow, we get more doublings. Eventually, we hit a chaotic
region -- there is no equilibrium, and the behaviour appears random. But
in this sea of chaos, there are strange islands of stability. There is a
cycle with period 3: a region of predictability in a sea of chaos.
So if you see a behaviour that has boom and bust cycles, or appears not
to be in equilibrium, there aren't necessarily peculiar or sinister forces
causing it. It might just be the natural behaviour implicit in a very
simple equation!
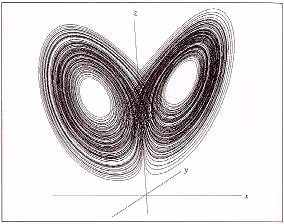 Lorenz
strange attractor
Lorenz
strange attractor
vx
= 10
x
- 10
y
vy
= 28
x
-
y
-
x z
vz
=
x y
- 8
z
/ 3
Here is a slightly more complicated set of equations. The speed in the
x
,
y
and
z
directions is given here. What sort of
behaviour does this describe?
[I ran a numerical simulation of the Lorenz
equations, allowing the solution to build up slowly. I talked through the
features as they appeared.]
The initial behaviour looks like a transient. We seem to be in a nice
cyclic place here. But wait! it's off somewhere. Now it's back. 3 times
round this loop, then twice round the other...
So, there are times when the behaviour is periodic and predictable, as
it cycles round one loop. And there are times when it flips to the other
cycle. And even times when it appears random.
These equations are a very simplified and cut-down versions of a simple
model of a weather system. So now you know why the weather may be so
difficult to predict -- it is a chaotic system.
The shape of this path is a fractal. There is a deep connection between
chaos and fractals.
Chaotic nanites
Nanites necessarily have small programs in them. And as we have see,
even such a small program could have incredibly bizarre behaviour.
But not
every
small program is chaotic. So why am I making all
this fuss? Isn't the answer just to choose those programs that aren't
chaotic?
Because we may need to exploit that very chaos to get what we need:
sufficiently complex behaviour. I will try to explain how ...
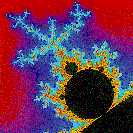 Mandelbrot
set
Mandelbrot
set
Let's look closer at fractals.
A fractal has the property of
self-similarity
. As you zoom in on
its structure, yet more structure appears, which is similar (but not
necessarily identical) to the higher level structure.
The Mandelbrot set is the classic example of a fractal.
[I
started a
Mandelbrot set
program, and
zoomed in a few times.]
The very simple generating equation,
z
n
+1
:=
z
n
2
+
c
implicitly contains infinite levels of structure.
Fractals everywhere
But fractals occur in the real world, too: it's not just Mandelbrot
sets!
-
If you look at a set of maps at different scales, coastlines always
look jagged. Coastlines are fractals.
-
River basins look fractal.
-
As do the pattern of blood vessels
-
If you examine the noise on telephone lines, the pattern is fractal
-
Even fluctuations in currency prices appear to be fractal.
Compression

With something like the Mandelbrot set, we have an enormously complex
image encoded in a very small equation. So we can describe the image very
simply. We say the image is
compressed
.
If we can go the other way -- start with a picture, find a fractal
equation that produces it -- we can compress images. This is done
routinely today -- many pictures you get on CD-ROMs use
fractal image compression
.
This might give us a clue about how DNA could hold enough information to
describe creatures. Human DNA is about 3 billion bases. You could fit a
complete description on a few CD-ROMs. There is software in existence of
this sort of size -- but it certainly doesn't describe anything as complex
as a person.
But we have seen that simple equations, simple algorithms, can describe
very complex results. And if you look at a map of veins and arteries, for
example, they look river-like, they look fractal. Maybe DNA contains a
fractally compressed description?
Programming a nanite
So this might give us a clue about how we can fit a large task into a
small program in a small nanite. We might need to use
fractal
algorithms
.
This is still an open research area -- how to go from the behaviour we
want to a compressed 'fractal algorithm' that encodes it.
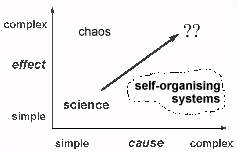 Self-organisation
Self-organisation
But this is only half the story. We want
trillions
of these
nanites to cooperate to build macroscopic objects. Do we have any hope of
controlling such a massively complex system?
There are indeed such things.
They are called self-organising systems, and they are everywhere, once
you know where to look.
Boolean networks
Consider a network of light bulbs.
Each bulb is randomly wired to 2 others, which act as input signals.
These inputs are fed through a random boolean function to say whether the
bulb should be on or off. For example, the function might say the bulb is
on only if both its inputs are on (the
AND
function), or if either is on (the
OR
function) or
is on all the time. There are 16 possible such functions.
Start the network off with bulbs lit randomly. Each generation,
determine the new state from its input state. The network has 2
N
possible different states, which for 400 bulbs is about a trillion
different states. So you might imagine, given everything has been set up
randomly, that the behaviour will look random, with bulbs flashing on and
off in no discernible pattern.
[Quick demo of 20x20
lights flashing at random.]
Let's watch what happens.
[Demonstration of a
Boolean network
.]
The pattern
settles down
very
quickly, to a cycle length of very much less
than
N
. This is truly
astonishing
! Totally unexpected
behaviour. The very complex system has self-organised into a simple
behaviour.
Aside: big numbers
Self-organising systems can involve huge numbers of separate components
-- millions of billions, if not more, of cooperating entities. It is
possible to visualise big numbers like these.
See this one litre carton here, it is 10cm on each side. Imagine marking
off one side in millimetres -- so there's a hundred of them. Now imagine
I've got a fine saw, and I saw along the marks, so the cube would be cut
up into 100 sheets, 1mm thick, and 10cm square. Now mark millimeters along
another edge. Imagine I saw it up again. Now I would have 100 squared, or
10,000, rods, 10cm tall, and 1mm thick. Now take the last side, and mark
off millimeters, and I cut again. Now I would have got a load of 1mm
cubes, 1 million of them! So you've just visualised a
million
.
Another way of seeing a million is to imagine this box filled up with
grit or coarse sand, each grain about a millimetre across. There would be
about a million grains of sand in here.
Imagine instead a 1 metre box, full of sand. That is a 1000 litres, so
there are about a billion grains of sand there. So you have just
visualised a
billion
. Imagine six of those boxes, and you have
visualised a grain of sand for every person on the planet!
[See also
Data
Powers of Ten
]
Emergent properties
Self-organising systems have
emergent properties
: something that
is a property of the system as a whole, not of any of the individual
components from which it is made. Emergent properties are simple
properties of complex systems, and they are often surprising and
unpredictable.
I'm going to show you how a system consisting of about a million
components can have a simple property.
[I slowly
poured out my one million grains, or litre, of sand onto the table.]
Notice how the slope of the sand pile stays roughly constant. If it is
shallower than this critical slope, it waits for more sand to pile up. If
it is steeper, avalanches occur. The system
self-organises
to a
constant slope.
Other examples of self-organising systems:
-
flocking behaviour
[I demonstrated a 'flocking
boids' program]
-
Saturn's rings
-
autocatalytic systems
-
life -- more than 'just' chemistry
-
intelligence -- more than 'just' a pile of neurons
At the "edge of chaos"
Many self-organising systems can be characterised by some parameter.
When this parameter is too small, the system is static, frozen, fixed.
When it is too large, the system is random, liquid, unstructured. But when
it is just right, the system is in transition between these two stages. It
has structures on all scales, and is "on the edge of chaos".
|
|
static
|
complex
|
random
|
|
physics
|
solid
|
phase-change
|
liquid
|
|
Boolean nets
|
sparse
|
2-way
|
dense
|
|
biology
|
non-life
|
life
|
death
|
|
economics
|
totalitarian
|
controlled
|
laissez-faire
|
|
computing
|
store
|
compute
|
process
|
-
physics -- parameter = temperature, critical region is a phase change
-
Boolean nets -- connectivity / small-period cycles
-
biology -- entropy / life
-
economics -- market deregulation / economic success
-
computing -- information flow / processing
The range of critical parameters is so very small, and you might think
it would be hard to find and to maintain. But many self-organising systems
seem to
evolve
themselves towards their critical parameter value.
If they are too static, they loosen up a bit. If they are too fluid, they
cool down a bit.
New perspective
For any complex system, including a system of nanites, to survive, it
must be flexible. It must be flexible enough that it isn't frozen solid,
but not so flexible that it is a random jumble.
What the study of complex self-organising systems is telling us is this.
To be just flexible enough, a system has to have following properties:
-
be highly dynamic, so not in equilibrium
-
be constantly evolving and changing, not steady state
-
be in a state of flux, not static
If a complex system does not have these properties, we have a name for
it:
dead
Trillions of nanites
So our problem is how to organise trillions of nanites to cooperate to
build some macroscopic object, without collapsing into random noise.
The study of self-organising systems offers us some hope in this area.
Complex systems
can
have simple behaviours. What is more, they
often spontaneously self-organise into these simple behaviours without any
outside control. But the flexible, dynamic, evolving behaviour such a
system must have doesn't yet fit in with the way we like to think about
engineering software.
So the open question, that we don't yet have an answer to, is this: we
know what property we want. How do we design a self-organising system that
has this as an emergent property?
The future
So, to summarise: Nanotechnology offers fantastic rewards. But before we
can reap those rewards, we have to solve at least two programming
problems:
-
Small programs for big tasks
. How do we fit small programs
into small nanites to perform complex tasks? Fractal algorithms may hold
the key. But we don't yet have any science of fractal program
compression
-
Many nanites make light work
. How do we get trillions of
nanites to work together? Self-organising systems may be the route here.
But we don't yet understand emergent properties, let alone how to design
systems to exhibit some required emergent property.
And least you think this is all too
science
fictional
to be taken seriously: these problems are not peculiar to
nanotechnology. They have to be solved if we are going to develop truly
versatile complex software for
whatever
purpose.
So these are the challenges. You here are the next generation of
scientists and engineers. Maybe some of you will solve them.
 Notes
and slides for a talk I gave on
complexity and
nanotechnology
at the University of Aston's
Computing for
the New Millennium
schools day, in January 1996. The audience were
mainly 15-16 year old school children, interested in science. The aim
of the day was to excite them about various whizzy science and
technology they may not have come across in their schools courses.
(Other talks included virtual reality and cryptography.)
Notes
and slides for a talk I gave on
complexity and
nanotechnology
at the University of Aston's
Computing for
the New Millennium
schools day, in January 1996. The audience were
mainly 15-16 year old school children, interested in science. The aim
of the day was to excite them about various whizzy science and
technology they may not have come across in their schools courses.
(Other talks included virtual reality and cryptography.)
 Natural
size scales
Natural
size scales
 Can we ever
get enough nanites to build something macroscopic? What are
self-replication timescales? We can make some very rough estimates, using
2
10
~ 10
3
, so every 10 doublings, we would have a
1000 times as many nanites
Can we ever
get enough nanites to build something macroscopic? What are
self-replication timescales? We can make some very rough estimates, using
2
10
~ 10
3
, so every 10 doublings, we would have a
1000 times as many nanites
 Grey
goo
Grey
goo

 Classical
dynamics: attractors
Classical
dynamics: attractors

 Chaos
Chaos

 Lorenz
strange attractor
Lorenz
strange attractor


 Self-organisation
Self-organisation