Testing as Abstraction
Susan Stepney
Logica UK Ltd
Copyright © 1995 Logica UK Ltd
Abstract
The PROST-Objects project has developed a method for formally specifying tests. The method is based on systematic abstraction from a 'state-plus-operation' style specification. It is explained here, and illustrated with a small example. Test developers can use this method, along with their own skills for choosing good tests, to produce a suite of formal test specifications. The project has also developed a prototype tool, which provides organisational support for the (potentially large) collection of test specifications as they are generated.
Introduction
On the one hand we have a Z specification of the behaviour of a system; on the other hand we have a purported implementation of that system. We want to test that the implementation conforms to the specification. To do this we need a test suite whose individual tests have good coverage and little overlap. The original specification is the obvious place to start in order to derive such a test suite.
The PROST-Objects project has developed a method for taking the formal specification of a system and systematically deriving from it formal specifications of conformance tests. This paper describes our method by using a small worked example; it also describes a prototype tool we have been building to support the method.
PROST-Objects is applying this method to the specifications of OSI Managed Objects, in order to derive specifications of tests that can be used to show that implementations of Managed Objects conform to their formal specifications.
The project is using ZEST, an object oriented extension to Z being developed at British Telecommunications' Research Labs [Cusack & Rafsanjani 1992]. However, the underlying method is not specific to object oriented specifications, or to Managed Object specifications. It is a general method applicable to plain Z specifications written in a 'state-and-operations' style, and is described here in those terms.
Test Suites
Testing is an essential part of the software development lifecycle. The existence of a formal specification can help reduce the burden of defining the tests, because it can be used to help derive a good test suite.
Here, we discuss a methodical (but not automatic) approach to deriving Z specifications of tests from Z specifications of operations.
We want to test that some system correctly implements the specification of some operation, Op. By 'correctly implements', we mean that for every specified before-state (including inputs), the implementation produces at least one of the specified after-states (including outputs), and not some other state or output.
In general, it is not possible to test exhaustively the entire state space, due to combinatorial explosion. Often it is not useful to test everything; many possible before-states are qualitatively similar to others, and so tests for these tell us nothing new. Also, it is not always useful to test that the entire after-state has been established as specified. For example, consider the specification of a query operation that outputs some value and leaves the state unchanged. It might be that only the value of the output is checked, and not that the state has been unaffected.
The process of building a test suite comprises selecting a 'useful' subset of the interesting before-states, and selecting those parts of the corresponding after-state to check.
There are various criteria for such a selection: it should give the best test coverage given limited testing resources; it should concentrate on the important parts of the implementation; it should identify bugs; .... These are all informal criteria, and it does not seem sensible to attempt to provide some automatic method to perform this selection. Indeed, attempts at automatic test generation can easily succeed in generating a copious number of trivial tests, but automatically generating pertinent tests has proved much more difficult. Rather than try to devise an automatic test generation method, our approach in PROST-Objects has been to develop a framework method within which test suite developers can apply their own skills, and to build prototype tool support to assist this process.
The method is described in the following sections, and the tool support in section ''Tool Support''.
The Test Method
Using our test method, a tester starts with the Z specification of an operation, Op say, and systematically manipulates it to produce a set of specifications of the relevant tests. Each test is itself specified by a Z operation schema. Our method is based on the following observations:
- We test only a subset of the interesting inputs and before-states. Such a test is captured by a specification OpTest that is less deterministic than the original specification of Op, because OpTest does not constrain the behaviour of states starting outside the tested subset.
- We test only some of the consequences of the state transition specified by Op, that is, examining only some outputs and a part of the after-state. Such a test is also captured by a specification that is less deterministic than Op's, because OpTest does not constrain the untested part of the after-state.
Our method produces test specifications by systematically introducing non-determinism into the original specification.
For example, consider the following file system specification, which has a state consisting of a mapping from file names to file contents, and the set of files open for reading.
[NAME, FILE]

This file system has a read operation that takes a list of NAMEs, and returns a corresponding list of FILEs. For each file, if it is open, the operation gives the actual contents, but if it is closed, or does not exist, the operation gives some error flag. (In order to keep this example simple, these error results have the same type as the file; this is not necessarily the best way to specify such a system for real.)
Consider how we might want to test a purported implementation of Read. Based on our (presumably short?) experience as a builder of file system test suites, we decide that we will test only open files, and only those file name lists of length one, #n?=1, and check that we get the correct single output in response. We decide not to test that the entire state remains unchanged, but we do want to check that the chosen file itself remains open after the read, because we have some suspicion that this might not be the case. So we specify our test as:
ReadTest is a less deterministic specification than Read.
The after-state is much less constrained than before:
![]() FileSys'
is constrained only to obey the predicates on FileSys', plus the
openness condition on n?1, whereas before it was completely
determined to have the same value as
FileSys'
is constrained only to obey the predicates on FileSys', plus the
openness condition on n?1, whereas before it was completely
determined to have the same value as ![]() FileSys.
Also, f! is constrained to have a particular value only when the
implication's antecedent, #n?=1 /\ n?1
FileSys.
Also, f! is constrained to have a particular value only when the
implication's antecedent, #n?=1 /\ n?1
![]() open,
is true, not for every value of n? as before.
open,
is true, not for every value of n? as before.
Putting this a more familiar way, Read is more deterministic than ReadTest, and hence Read is a refinement of ReadTest. Equivalently, ReadTest is an abstraction of Read. We use this insight of the existence of an abstraction relation between operations and their tests in our method for structuring the test discovery process.
Preamble and Checking Phases
There is one more step to be taken after specifying a test like ReadTest, before we can perform the test. How do we know that the file exists, and is open, before the operation? How do we know that the f! output from our ReadTest is the correct value? And how do we know that the file is still open after the operation?
We know because during the preamble to the test, before we perform (our implementation of) ReadTest, we open the file and set its contents to some known value to compare against f!. And later, during the checking phase of the test, we interrogate the open status of the file.
So a complete specification for performing and checking a test has the following structure:
ReadTestc
Preamble
ReadTest
Check
Here Preamble and Check are combinations of operations that put the system into some known state, and query the system's state, respectively.
The rest of this paper discusses the building of ReadTest. Specifying Preamble and Check is also being investigated by PROST-Objects.
Structuring the Test Suite
Although for the simple example given above it is possible to write down the final version of the desired test, the task is not so simple for a real world specification. Also, a single operation will likely have many different tests defined, testing different aspects of its behaviour. We would like some systematic way for deriving and documenting these tests, and we would like to get some idea of test coverage; some idea of what is not being tested.
This is what the test method that we have developed in the PROST-Objects project does. The method provides a set of well-defined actions, which can be performed at each stage of the process, building successively more abstract operations. These operations are structured as a tree of specifications, with the original operation at the root, and the tests at the leaves. Starting from the specification of a single operation, test developers working with the method select an appropriate action to perform at each stage, in order to reach a good set of tests. Which action to choose is part of the tester's skill, and is not the subject of this paper.
The method defines various actions to be used in developing the tests: partitioning, weakening, and simplification, described below. Our prototype tool, described later, provides support for each of these actions. The method also provides heuristics that reduce the need to discharge various proof obligations.
Proof obligations
Once the tree of specifications has been built in accordance with the method, the set of all the leaves comprises the specifications of the tests. Each time we apply an action, we divide an operation into several parts, each of which will either form a test, or be further divided. The allowed division is not arbitrary, but must satisfy the following correctness conditions (here C is the current specification being abstracted from; Ti are the tests produced at this step:
- Soundness: As noted above, the test method is based on a
refinement/abstraction relation holding between a specification and each
of its tests. For total operations, this reduces to the set of
conditions:
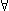 i
i  C
C  Ti
Ti - Completeness: Nothing must be lost when deriving the
specification of the tests. The conjunction of all the leaves must be
equivalent to the original specification. (For an explanation of why the
tests are conjoined, rather than disjoined, see appendix.)
C = /\i Ti
Each leaf is the specification of a single test. We have some 'niceness' conditions that allow us to ensure we do not specify too many tests, and allow us to interpret the meaning of failing a test, or of not performing a test. These criteria can be understood by considering the set of specifications ¬Ti. Any system that implements ¬Ti fails to implement the specification Ti.
- Independence: No test should be redundant: it should test at
least something not covered somewhere in another test. Test j is
independent of all theother tests if the specification ¬Tj
is not wholly contained in the union of the other ¬Ti
specifications:
This simplifies to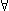 j
j  ¬ (¬Tj
¬ (¬Tj
 \/{i
\/{i  j}¬Ti
)
j}¬Ti
)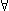 j
j  ¬ ( /\{i
¬ ( /\{i
 j} Ti
j} Ti
 Tj )
Tj ) - Orthogonality: Ideally, we would like the tests to have no
overlap at all. This would mean that an implementation could fail at
most one test, and that any test designated as a residual would specify
precisely what is not being tested (would be 'honest'). The tests are
orthogonal if the specifications of ¬Ti
are disjoint:
which simplifies to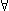 i
i  j
j  ¬ (¬Ti
/\ ¬Tj
)
¬ (¬Ti
/\ ¬Tj
)
Orthogonality is a very strong condition. It is convenient to relax it to orthogonal 'up to' a predicate, for example, up to (the implicit predicate in) a declaration.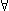 i
i  j
j  Ti \/
Tj
Ti \/
Tj
In general, discharging such proof obligations would be quite onerous. However, in practice the choice of division is not arbitrary, but governed by the form of the specification being divided. Certain choices can reduce the complexity of the required proofs. In addition, the method describes certain special cases, which automatically satisfy some proof obligations. Use of these special cases substantially reduces the proof burden to a manageable level.
Partitioning
A set of less deterministic operations is derived from the current version of the operation by partitioning the input space and before-state. This gives a set of operation definitions each covering part of the before-state.
C
T1 /\ ... /\ Tn
For example, the first step in defining the tests for Read could be a partitioning of the input n? on the length of the sequence:
- #n? = 0
- #n? = 1
- #n? > 1
Other partitions on the length of the sequence might be chosen. For example, if sequences of length two were thought to be deserving of special attention, this might be included explicitly as an extra partition #n?=2 (and changing the last partition to #n?>2).
Once a suitable n-way partition has been decided, in the form of n predicates Hi, n sound abstract operations are defined, each of the form
C
[ D | P ]
Ti
[ D | Hi
P ]
So, for the case of #n?=1, we get
The choice of the term 'partition' for this action gives a clue to a heuristic for satisfying the proof obligations: the tests are sound by construction, and if the predicates Hi do partition the space, then the operations combine to form the original, and do not overlap. That is, the completeness proof obligation is satisfied if \/i Hi, and additionally the tests are orthogonal (up to the declaration) if
i
j
¬ (Hi /\ Hj )
These conditions hold for the choice of partition in our example. So we have
Read
ReadNone /\ ReadOne /\ ReadMany
Simplification
The action of partitioning by textually replacing P by H ![]() P
usually leads to a specification that can be written in a simpler form
(since in practice H is not an arbitrary predicate, but governed
by the form of the declaration or of P). H may be assumed
in P and used to simplify it. For example, assuming #n? = 1
in ReadOne enables us to remove the quantifier and give a more
explicit form for the sequence f!:
P
usually leads to a specification that can be written in a simpler form
(since in practice H is not an arbitrary predicate, but governed
by the form of the declaration or of P). H may be assumed
in P and used to simplify it. For example, assuming #n? = 1
in ReadOne enables us to remove the quantifier and give a more
explicit form for the sequence f!:
We have a proof obligation to show that the simplification does not alter the meaning of the schema.
Here we have
ReadOneSimp
ReadOne
Having simplified the schema, we look to see which action to perform next. Another partitioning of the input, this time on whether the name corresponds to an open, closed, or unknown file, seems a good choice.
- n?1
 open
open - n?1
 dom fsys \ open
dom fsys \ open - n?1
 dom fsys
dom fsys
The open case gives us, remembering that A![]() (B
(B![]() C)
C) ![]() A/\B
A/\B ![]() C,
C,
Simplifying this, using A/\B ![]() (B
(B![]() C)
C) ![]() A/\B
A/\B ![]() C,
gives
C,
gives
Weakening
The final action defined by the PROST-Objects method is to loosen the constraints on the after-state. This action results in the definition of two (or more) operations: one that loosens the constraints as appropriate for the test, and one (or more) that contains the residual part of the definition, the part of the operation not being tested.
C
Tw /\ Tr
Before weakening ReadOneOpen, it helps to 'simplify' it by
exposing the hidden predicates in ![]() FileSys,
because in this case, it is these predicates that are to be weakened.
Since we are going to check that the read file remains open, but not that
any other file does, we also split up the predicate open=open'
into three separate predicates.
FileSys,
because in this case, it is these predicates that are to be weakened.
Since we are going to check that the read file remains open, but not that
any other file does, we also split up the predicate open=open'
into three separate predicates.
We simplify this, using (A![]() B)/\(A/\C
B)/\(A/\C ![]() D)
D) ![]() A
A![]() B/\(C
B/\(C![]() D),
to
D),
to
We are now in a position to weaken this definition, by choosing just the last predicate
We take the residual to be of the form Tr=Tw![]() C,
which gives a residual orthogonal up to the declaration. After
simplification, this is:
C,
which gives a residual orthogonal up to the declaration. After
simplification, this is:
This choice is not the only pattern for weakening an operation. There are other ways of weakening that are useful, and that also satisfy the proof obligations. For example, the proof obligations are automatically satisfied if we choose any one of
| 1. | C = A /\ B | : | Tw = A , | Tr = A
|
|
| 2. | C = A /\ B | : | Tw = A \/ B , | Tr = A
|
|
| 3. | C = A |
: | T1 = A
|
T2 = B
|
|
| 4. | C = A /\ B | : | Tw = A \/ B , | T1 = A
|
T2 = B
|
(Case 4 is a combination of cases 2 and 3. It is interesting because it
allows the non-orthogonal tests A and B to be used, by the
identities A = (A\/B)/\(B![]() A)
and similarly for B.)
A)
and similarly for B.)
Our example falls into case 1.
Test Coverage
![[example tree of specifications]](tree.gif)
Figure 1. The example tree of specifications. The specifications to the right of a link are abstractions of the specifications to the left. Partitions are shown as bold links, simplifications as dashed links, and weakenings as light links. Test leaves are shown as bold boxes, and residuals as dashed boxes.
The residuals document what is not being tested. In the example above,
let's assume that ReadOneOpenTest is the only test, and all the
other leaves in the tree of specifications (see figure 1)
are residuals. So the residuals at the first partitioning explicitly
document that input sequences of length zero, and length greater than one,
are not being tested. At the next partitioning we learn that (for
sequences of length one) closed and non-existent files are not being
tested. And at the weakening, we learn that three things are not being
tested: that the file system is unchanged (from fsys=fsys'), that
the subset of open files other than n?1 is unchanged (from open
\ {n?1} = open' \ {n?1}), and that for n?1,
that if it is open after then it was open before (from n?1
![]() open'
=> n?1
open'
=> n?1 ![]() open).
open).
Reusing the Test Suite
The specification being used to generate the tests could itself be a refinement of some other pre-existing specification. For example, the specifications of a family of related products may be structured in such a way [Garlan & Delisle 1990], [Garlan & Notkin 1991]. Managed Object specifications form one such family.
If such a refinement relation exists, and if the other specification already has some tests defined, then those tests are valid tests for the new specification also (because abstraction is transitive).
This greatly reduces the burden on the test suite designer. New tests need be defined only for the new part of the specification, for example, extra operations, or extended parts of preconditions (in our interpretation, those before-states which were previously in the maximally non-deterministic 'unconstrained' region, but which have been refined into the 'interesting' region; see appendix). All the common parts of the specification are already tested by the pre-existing tests. Exploiting this reuse is a key feature of our structure for tests in PROST-Objects. The structure is difficult to capture formally using plain Z, but our ZEST specifications naturally fall in a refinement hierarchy, which is expressed as inheritance.
Testing ZEST class specifications
ZEST [Cusack & Rafsanjani 1992] is an object oriented extension to Z, particularly suited to the specification of Managed Objects [Wezeman & Judge 1994]. We are using it in PROST-Objects to specify both Managed Objects and their tests.
In ZEST, subclassing replaces the concept of refinement (the two concepts are not identical, but are close enough for our purposes) [Hall 1994]. So the abstract tests are parent classes of the tested class specification. We can use inheritance to capture, formally within a specification, the abstraction relation between tests described above. The inheritance tree also provides a framework for documenting the decisions made when building the tests for an object.
If the class specification under test is itself a child of another class, then its parent's tests are also valid tests for itself. Our test method enables us to include all parents' tests in the test suite. Not only can parents' tests themselves be reused, but the testing strategy---the choices of partitioning and weakening made at each step---can also be reused.
Tool Support
Many hundreds, or even thousands, of tests may well be needed for a real-world specification. Doing this systematically on paper (using any method, not just ours!) is time consuming, excruciatingly tedious, and error-prone; tool support is essential to make systematic test generation economically viable.
Under PROST-Objects, we are developing prototype tool support for our test method. This tool, called Zylva, provides support for the method actions of partitioning, simplifying, weakening, and for reusing parents' tests.
Zylva allows the tester to build a tree of specifications related by inheritance. (See figure 2.) The tool is built around a navigator, which allows movement around the existing test tree structure, and provides provides special subtools for partitioning, simplifying, and weakening, in order to grow and edit the tree. The tree structure is shown graphically; the kind of branch (Partition, Simplification, or Weakening) is indicated by colour; at each branch the status of the proof obligations (discharged or not) is indicated by the line style; the status of the leaves (unfinished, test purpose, residual, or parent tests) is indicated by box shape.
Figure 2. A screen shot of Zylva, showing the Navigator (top left), the Partitioner (top right), a ZEST-Formaliser editor (bottom left), and a Symbol Palette (bottom right).
When a new set of parents is created by one of the subtools, some of the proof obligations are satisfied automatically by construction; the others need further work to be discharged. Also, editing a node in the middle of the tree causes potential inconsistencies, due to the nature of the proof obligations between various specifications. The navigator maintains a record of the current status, and of any potential inconsistencies introduced by such editing, and propagates them up the tree as necessary as the proof obligations are discharged.
Zylva's partitioner includes a 'hinter' option, that can suggest a suitable partition based on the structure of the input, state, or predicate. For example, it has built-in knowledge about sequences, and so can provide the 'zero, one, many' hint automatically. These hints can be edited by the tester, for example, by adding an extra #n?=2 case, and reused in other partitions. As we discover kinds of partitions useful for real Managed Object specifications during the course of the project, we will make the hinting strategy more sophisticated. Once the tester has decided on the appropriate hints, Zylva automatically creates one sound class per hint.
Zylva's simplifier provides a ZEST-Formaliser editor on a copy of the operation, which allows the test builder to perform the simplification. Formaliser is a generic formal specification tool [Flynn et al. 1990]; a version has been instantiated with ZEST's grammar and type system for PROST-Objects.
Zylva's weakener provides a ZEST-Formaliser editor on a copy of the operation, which allows the test builder to perform the weakening, usually by deleting unwanted predicates. Once the tester has performed the appropriate weakening, Zylva automatically creates the complete, orthogonal residual class. The residual is sound if the weakened class is sound (which it is if the weakening consisted of deleting predicates).
Conclusions
The insight that a test is an abstraction of an operation can be used to structure a hierarchy of tests. The PROST-Objects test method
- provides rules for building and structuring this hierarchy
- suggests heuristics that minimise the proof obligations
- makes explicit the parts of the specification not being tested
- maximises reuse of tests between related specifications
The Zylva test tool provides direct support for the actions defined by the method. It also provides, by construction, partial automatic satisfaction of the proof obligations in the following cases:
| Partitioner | Weakener, with
Tr = Tw |
|
| sound | yes | Tr sound if Tw sound |
| complete | if \/i Hi | yes |
| orthogonal | if ¬ (Hi /\ Hj) | yes |
Such tool support relieves test builders of much of the low-level burden of defining tests, allowing them to concentrate on the skillful part: deciding just what are the 'good' tests.
Acknowledgements
PROST-Objects is a collaborative research project awarded by the United Kingdom's Department of Trade and Industry as part of its PROST programme (Programme of Research into Open System Testing). The partners are British Telecommunications plc, Logica UK Limited, and National Computer Centre Limited. The work described in this paper is the joint effort of all the team members on the project. Further work from the PROST-Objects project team is described elsewhere in this proceedings [Strulo 1995].
References
- [Bowen & Hall 1994]
- Jonathan P. Bowen and J. Anthony Hall, editors. Proceedings of the 8th Z User Meeting, Cambridge 1994, Workshops in Computing. Springer Verlag, 1994.
- [Cusack & Rafsanjani 1992]
- Elspeth Cusack and G. H. B. Rafsanjani. ZEST. In Susan Stepney, Rosalind Barden, and David Cooper, editors, Object Orientation in Z, Workshops in Computing, chapter 10, pages 113--126. Springer Verlag, 1992.
- [Flynn et al. 1990]
- Mike Flynn, Tim Hoverd, and David Brazier. Formaliser---an interactive support tool for Z. In John E. Nicholls, editor, Z User Workshop: Proceedings of the 4th Annual Z User Meeting, Oxford 1989, Workshops in Computing, pages 128--141. Springer Verlag, 1990.
- [Garlan & Delisle 1990]
- David Garlan and Norman Delisle. Formal specifications as reusable frameworks. In Dines Bjørner, C. A. R. Hoare, and H. Langmaack, editors, VDM'90: VDM and Z---Formal Methods in Software Development, Kiel, volume 428 of Lecture Notes in Computer Science, pages 150--163. Springer Verlag, 1990.
- [Garlan & Notkin 1991]
- David Garlan and David Notkin. Formalizing design spaces: Implicit invocation mechanisms. In S. Prehn and W. J. Toetenel, editors, VDM'91: Formal Software Development Methods, Noordwijkerhout, Volume 1: Conference Contributions, volume 551 of Lecture Notes in Computer Science, pages 31--44. Springer Verlag, 1991.
- [Hall 1994]
- J.Anthony Hall. Specifying and interpreting class hierarchies in Z. In [Bowen & Hall 1994], pages 120--138.
- [Josephs 1991]
- Mark B. Josephs. Specifying reactive systems in Z. Technical Report TR-19-91, Programming Research Group, Oxford University Computing Laboratory, 1991.
- [Strulo 1995]
- Ben Strulo. How firing conditions help inheritance. In Jonathan P. Bowen and Michael G. Hinchey, editors, ZUM'95: 9th International Conference of Z Users, Limerick 1995, Lecture Notes in Computer Science. Springer Verlag, 1995.
- [Wezeman & Judge 1994]
- Clazien Wezeman and Tony Judge. Z for Managed Objects. In [Bowen & Hall 1994], pages 108--119.
Appendix: An Aside on Interpretation
Consider a schema Op that defines a relation between before-states State and after-states State' (we ignore inputs and outputs for the moment; the argument easily generalises). The before-states State can be partitioned into three regions:
- 'empty' region
- For these values of before-states the Op relation defines no
after-state.
{ State | ¬(
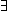 State'
State'  Op ) }
Op ) } - 'unconstrained' region
- For these values of before-states the Op relation allows any
valid after-state.
{ State | (
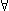 State'
State'  Op ) }
Op ) } - 'interesting' region
- For these values of before-states the Op relation allows
some, but not all, valid after-states.
{ State | (
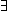 State'
State'  Op ) /\ (
Op ) /\ (
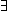 State'
State'  ¬Op ) }
¬Op ) }
The conventional interpretation of the schema Op as an operation is that in the 'empty' region, ''anything can happen, including things outside the scope of specification''. There is no formal distinction between the 'interesting' and 'unconstrained' regions, and the interpretation is that in these regions, ''any one of the specified after-states occurs'', which in the case of the 'unconstrained' region, means any state consistent with the state invariant.
In PROST-Objects, we choose to use a different interpretation. We interpret 'empty' to mean ''the operation is forbidden''; this interpretation is sometimes called the 'firing condition' or 'enabling condition' interpretation [Josephs 1991]. We also make a distinction between the 'interesting' and 'unconstrained' regions. The tests defined in this paper are tests of the 'interesting' region only. We choose not to test the 'unconstrained' region; by definition any result is allowed, and so our test could not tell us anything useful. (Under our interpretation, we should also test the 'empty' region, to ensure the operation indeed cannot happen here. This aspect of 'negative' testing is not covered in this paper.)
We have chosen to use the firing condition interpretation in order to make some of our definitions simpler. Because of this choice, our operations tend to be written as implications, with the antecedents defining (part of) the 'interesting' region. This allows alternative partitions of the operation to be '/\-ed' together (as opposed to '\/-ed' together in the conventional interpretation), which fits in with the way we define inheritance when we move to an object oriented formalism.
This interpretation also allows us to specify and refine 'uncontrolled' operations that may occur spontaneously, but only when their firing condition is true [Strulo 1995]. Such operations are essential for our application area, Managed Objects, but they are not expressible under the conventional interpretation without resorting to 'tricks'.










![[screen shot]](zylva.jpg)